Class 9 SEBA Maths (Assamese Medium)-Complete Study Material:
পুণৰালোচনা(Revision): Class 9 Maths R-1 Assamese Medium.
In this article, we have provided detailed solutions for SEBA Class 9 Maths Assamese Medium Question Answer R-1 (পুণৰালোচনা). We hope this article, ‘Class 9 Maths Assamese Medium Question Answer,’ will help you in your studies. If you have any doubts about this lesson পুণৰালোচনা, please visit our doubt section and ask your questions. We are ready to help you.

SEBA Class 9 Maths: পুণৰালোচনা
অনুশীলনী-R-1
পুণৰালোচনা Class 9 Maths Q1.
বৰ্গমূলৰ দ্বাৰা \( \sqrt{2} \) ৰ আনুমানিক মান দুই দশমিক স্থানলৈ উলিওৱা ।
সমাধানঃ

\(\therefore \sqrt{2} \) ≈ 1.41 ( 2 দশমিক স্থানলৈ)
পুণৰালোচনা Class 9 Maths Q2.
দুটা অপৰিমেয় সংখ্যা লিখা যাৰ যোগফল পৰিমেয় আৰু পূৰণফল পৰিমেয় ।
সমাধানঃ 4 + \( \sqrt{5} \) আৰু 4 – \( \sqrt{5} \)
Note: যোগফল পৰিমেয় আৰু পূৰণফল পৰিমেয় হোৱা দুটা অপৰিমেয় সংখ্যা সদায় \(a\) + \( \sqrt{b} \) আৰু \(a\) – \( \sqrt{b} \), b≥0 আৰ্হিৰ হ’ব ।
যোগফলঃ (4 + \( \sqrt{5} \)) + (4 – \( \sqrt{5} \) )
= 4 + 4
= 8 , পৰিমেয় ।
পূৰণফলঃ (4 + \( \sqrt{5} \)) × (4 – \( \sqrt{5} \) )
= \( 4^2 \) – \( (\sqrt{5})^2 \)
= 16 – 5
= 11, পৰিমেয় ।
পুণৰালোচনা Class 9 Maths Q3.
সংখ্যাৰেখাৰ সহায়ত 5 আৰু – 5 অৰ মধ্যৱৰ্তী অখণ্ড সংখ্যাবোৰ লিখা ।
সমাধানঃ
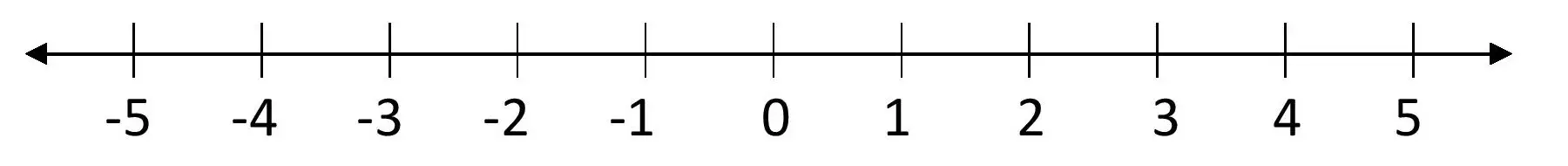
\(\therefore\) – 5 আৰু 5 ৰ মাজত থকা অখণ্ড সংখ্যাবোৰ হ’ল- – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4.
পুণৰালোচনা Class 9 Maths Q4.
সূচক বিধি \(a^m\) ÷ \(a^n\) = \( a^{m-n} \) অত m = n লৈ প্ৰমাণ কৰা যে \(a^0\) =1 ।
সমাধানঃ
দিয়া আছে, m = n
এতিয়া, \(a^m\) ÷ \(a^n\) = \( a^{m-n} \)
⇒ \(\frac{a^m}{a^n}\) = \( a^{m-n} \)
⇒\(\frac{a^n}{a^n}\) = \( a^{n-n} \) (\(\because m=n \))
⇒ 1 = \(a^0\)
⇒ \(a^0\) = 1
প্ৰমাণিত
পুণৰালোচনা Class 9 Maths Q5.
সূচক বিধি \(a^m\) ÷ \(a^n\) = \( a^{m-n} \) অত m = 0 লৈ প্ৰমাণ কৰা যে \(a^{-n} \) = \(\frac{1}{a^n}\) ।
সমাধানঃ
দিয়া আছে, m = 0
এতিয়া, \(a^m\) ÷ \(a^n\) = \( a^{m-n} \)
⇒ \(\frac{a^m}{a^n}\) = \( a^{m-n} \)
⇒ \(\frac{a^0}{a^n}\) = \( a^{0-n} \) (\(\because m=0 \))
⇒ \(\frac{1}{a^n}\) = \( a^{-n} \) ( \(\because a^{0} = 1 \))
⇒ \( a^{-n} \) = \(\frac{1}{a^n}\) প্ৰমাণিত
পুণৰালোচনা Class 9 Maths Q6.
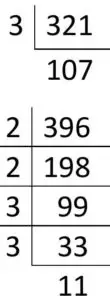
তলৰ যোৰৰ প্ৰত্যেকৰে মৌলিক উৎপাদক উলিয়াই গ.সা.উ(H.C.F) আৰু ল.সা.গু(L.C.M) থিৰ কৰা ।
(i) 321, 396 (ii) 455, 42 (iii) 408, 170
সমাধানঃ
(i) 321, 396
321 = 3 × 107
396 = 2×2 × 3 × 3 × 11
∴ গ.সা.উ = 3
ল.সা.গু = 2×2×3×3×11×107
= 42372
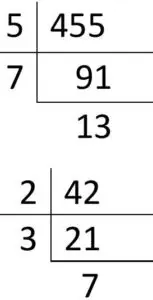
(ii) 455, 396
455 = 5 × 7 × 13
42 = 2 × 3 × 7
∴ গ.সা.উ = 7
ল.সা.গু = 2×3×5×7×13
= 2730
(iii) 408, 170
408 = 2 × 2 × 2 × 3 × 17
170 = 2 × 5 × 17
∴ গ.সা.উ = 2 ×17 = 34
ল.সা.গু = 2×2×2×3×5×17
= 2040

পুণৰালোচনা Class 9 Maths Q7.
\(\frac{2}{11}\) আৰু \(\frac{1}{6}\) ৰ মাজৰ দুটা পৰিমেয় সংখ্যা লিখা ।
সমাধানঃ
প্ৰদত্ত ভগ্নাংশ দুটাৰ হৰ 11 আৰু 6 ৰ ল.সা.গু = 6 × 11 = 66
এতিয়া,
\(\frac{2}{11}\) =\(\frac{2×6}{11×6}\) = \(\frac{12}{66}\)
\(\frac{1}{6}\) = \(\frac{1×11}{6×11}\) = \(\frac{11}{66}\)
আকৌ,
\(\frac{12}{66}\) = \(\frac{12×3}{66×3}\) = \(\frac{36}{198}\)
\(\frac{11}{66}\) =\(\frac{11×3}{66×3}\) = \(\frac{33}{198}\)
∴ \(\frac{2}{11}\) আৰু \(\frac{1}{6}\) ৰ মাজৰ দুটা পৰিমেয় সংখ্যা হ’ল- \(\frac{35}{198}\) আৰু \(\frac{34}{198}\) ।
**Note: এই প্ৰশ্নটোৰ অন্য শুদ্ধ উত্তৰো গ্ৰহণযোগ্য হ’ব ।
পুণৰালোচনা Class 9 Maths Q8.
সৰল কৰাঃ \(\sqrt{10} \times \sqrt{5}\)
\(\sqrt{2} = 1.41\) হ’লে প্ৰদত্ত সংখ্যাৰ আসন্ন মান কি হ’ব ?
সমাধানঃ
\(\sqrt{10} \times \sqrt{5}\)
= \(\sqrt{2×5} \times \sqrt{5}\)
= \(\sqrt{2} \times \sqrt{5} \times \sqrt{5}\)
= \(\sqrt{2} \times 5\) [\(\because\)\(\sqrt{5} \times \sqrt{5}\) = 5]
= \(5\sqrt{2}\)
আকৌ, \(\sqrt{2} = 1.41\) হ’লে
\(5\sqrt{2}\)
= \(5 \times 1.41\)
= 6.05
পুণৰালোচনা Class 9 Maths Q9.
\(\frac{p}{q}\) আৰ্হিৰ ভগ্নাংশত প্ৰকাশ কৰাঃ
(i) \(0.\overline{81}\) (ii) \(0.1\overline{8}\) (iii) \(2.4\overline{7}\) (iv) \(2.44\overline{31}\)
সমাধানঃ
(i) \(0.\overline{81}\)
ধৰা হ’ল,
\(x = 0.\overline{81}\) ——›(1)
⇒ \(100 \times x = 100\times 0.\overline{81}\)
⇒ \(100x = 81.\overline{81}\)
⇒ \(100x = 81 + 0.\overline{81}\)
⇒ \(100x = 81 + x\) [from (1)]
⇒ \(100x \ – \ x = 81 \)
⇒ \(99x = 81 \)
⇒ \(x = \frac{81}{99}\)
⇒ \(x = \frac{9}{11}\)
(ii) \(0.1\overline{8}\)
ধৰা হ’ল,
\(x = 0.1\overline{8}\) ——–›(1)
⇒ \(10 \times x = 10\times 0.1\overline{8}\)
⇒ \(10x = 1.\overline{8}\)
⇒ \(10x = 1.7 + 0.1\overline{8}\)
⇒ \(10x = 1.7 + x \) [from (1)]
⇒ \(10x \ – \ x = 1.7 \)
⇒ \(9x = 1.7 \)
⇒ \(x = \frac{1.7}{9}\)
⇒ \(x = \frac{17}{90}\)
(iii) \(2.4\overline{7}\)
ধৰা হ’ল,
\(x = 2.4\overline{7}\) ——–›(1)
⇒ \(10 \times x = 10 \times 2.4\overline{7}\)
⇒ \(10x = 24.\overline{7}\)
⇒ \(10x = 22.3 + 2.4\overline{7}\)
⇒ \(10x = 22.3 + x\) [from (1)]
⇒ \(10x \ – \ x = 22.3 \)
⇒ \(9x = 22.3 \)
⇒ \(x = \frac{22.3}{9} \)
⇒ \(x = \frac{223}{90} \)
(iv) \(2.44\overline{31}\)
ধৰা হ’ল,
\(x = 2.44\overline{31}\) ——›(1)
⇒ \(100 \times x = 100 \times 2.44\overline{31}\)
⇒ \(100x = 244.\overline{31}\)
⇒ \(100x = 241.87 + 2.44\overline{31}\)
⇒ \(100x = 241.87 + x\) [from (1)]
⇒ \(100x \ – \ x = 241.87 \)
⇒ \(99x = 241.87 \)
⇒ \(x = \frac{241.87}{99} \)
⇒ \(x = \frac{24187}{9900} \)
পুণৰালোচনা Class 9 Maths Q10.
সৰল কৰাঃ
(i) \((\sqrt{3} \ – \sqrt{2})^2\)
সমাধানঃ
\((\sqrt{3} \ – \sqrt{2})^2\)
\(= (\sqrt{3})^2 \ – \ 2.\sqrt{3}.\sqrt{2} + (\sqrt{2})^2\)
\(= 3 \ – \ 2\sqrt{6} + 2\)
\(= 5 \ – \ 2\sqrt{6}\)
(ii) \((2\sqrt{3} \ + \sqrt{5}) (2\sqrt{3} \ – \sqrt{5})\)
সমাধানঃ
\((2\sqrt{3} \ + \sqrt{5}) (2\sqrt{3} \ – \sqrt{5})\)
\(= (2\sqrt{3})^2 \ – \ (\sqrt{5})^2\)
\(= 12 \ – \ 5\)
\(= 7\)
(iii) \((8 + \sqrt{3}) (2 + \sqrt{3}) \)
সমাধানঃ
\((8 + \sqrt{3})(2 + \sqrt{3})\)
\(= 8 \cdot 2 + 8 \cdot \sqrt{3} + \sqrt{3} \cdot 2 +(\sqrt{3})^2 \)
\(= 16 + 8\sqrt{3} + 2\sqrt{3} + 3\)
\(= 16 + 3 + (8\sqrt{3} + 2\sqrt{3})\)
\(= 19 + 10\sqrt{3}\)
(iv) \(\frac{1}{1 + \sqrt{2}} \)
সমাধানঃ
\(\frac{1}{1 + \sqrt{2}} \ × \frac{1 – \sqrt{2}}{1 – \sqrt{2}}\)
\(= \frac{1 – \sqrt{2}}{(1 + \sqrt{2})(1 – \sqrt{2})}\)
\(= \frac{1 – \sqrt{2}}{1^2 – (\sqrt{2})^2}\)
\(= \frac{1 – \sqrt{2}}{1 – 2}\)
\(= \frac{1 – \sqrt{2}}{-1}\)
\(= \sqrt{2} – \ 1\)
(v) \(\frac{4}{\sqrt{7} + \sqrt{3}} \)
সমাধানঃ
\(\frac{4}{\sqrt{7} + \sqrt{3}} \ × \frac{\sqrt{7} – \sqrt{3}}{\sqrt{7} – \sqrt{3}}\)
\(= \frac{4(\sqrt{7} – \sqrt{3})}{(\sqrt{7})^2 – (\sqrt{3})^2}\)
\(= \frac{4(\sqrt{7} – \sqrt{3})}{7 – 3}\)
\(= \frac{4(\sqrt{7} – \sqrt{3})}{4}\)
\(= \sqrt{7} – \sqrt{3}\)
(vi) \(\frac{7 + \sqrt{3}}{7 – \sqrt{3}} \)
সমাধানঃ
\(\frac{7 + \sqrt{3}}{7 – \sqrt{3}} \ × \frac{7 + \sqrt{3}}{7 + \sqrt{3}}\)
\(= \frac{(7 + \sqrt{3})^2}{(7)^2 – (\sqrt{3})^2}\)
\(= \frac{7^2 + 2.7.\sqrt{3} + (\sqrt{3})^2}{49 – 3}\)
\(= \frac{49 + 14\sqrt{3} + 3}{46}\)
\(= \frac{52 + 14\sqrt{3}}{46}\)
\(= \frac{26 + 7\sqrt{3}}{23}\)
(vii) \( \frac{1}{1 + \sqrt{2}} \) + \(\frac{1}{\sqrt{2} + \sqrt{3}}\) + \(\frac{1}{\sqrt{3} + \sqrt{4}}\)
সমাধানঃ
\( \frac{1}{1 + \sqrt{2}}\) + \(\frac{1}{\sqrt{2} + \sqrt{3}}\) + \(\frac{1}{\sqrt{3} + \sqrt{4}}\)
\(= \frac{1}{1 + \sqrt{2}} ×\frac{1 – \sqrt{2}}{1 – \sqrt{2}} \) + \(\frac{1}{\sqrt{2} + \sqrt{3}} × \frac{\sqrt{2} – \sqrt{3}}{\sqrt{2} – \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} × \frac{\sqrt{3} – \sqrt{4}}{\sqrt{3} – \sqrt{4}}\)
\(=\frac{1 – \sqrt{2}}{(1)^2 – (\sqrt{2})^2}\) + \( \frac{\sqrt{2} – \sqrt{3}}{(\sqrt{2})^2 – (\sqrt{3})^2}\) + \( \frac{\sqrt{3} – \sqrt{4}}{(\sqrt{3})^2 – (\sqrt{4})^2}\)
\(=\frac{1 – \sqrt{2}}{1 – 2} + \frac{\sqrt{2} – \sqrt{3}}{2 – 3} + \frac{\sqrt{3} – \sqrt{4}}{3 – 4}\)
\(=\frac{1 – \sqrt{2}}{-1} + \frac{\sqrt{2} – \sqrt{3}}{-1} + \frac{\sqrt{3} – \sqrt{4}}{-1}\)
\(= \sqrt{2} – 1 + \sqrt{3} – \sqrt{2} + \sqrt{4} – \sqrt{3}\)
\(= -1 + \sqrt{4}\)
\(= -1 + 2 = 1\)
(viii) \(\frac{\sqrt{a+x} – \sqrt{a-x}}{\sqrt{a+x} + \sqrt{a-x}}\)
সমাধানঃ \(\frac{\sqrt{a+x} – \sqrt{a-x}}{\sqrt{a+x} + \sqrt{a-x}}\)
\(=\frac{\sqrt{a+x} – \sqrt{a-x}}{\sqrt{a+x} + \sqrt{a-x}} × \frac{\sqrt{a+x} – \sqrt{a-x}}{\sqrt{a+x} – \sqrt{a-x}}\)
\(= \frac{(\sqrt{a+x} – \sqrt{a-x})^2}{(\sqrt{a+x})^2 – (\sqrt{a-x})^2}\)
\(= \frac{(a+x) – 2\sqrt{(a+x)(a-x)} + (a-x)}{(a+x) – (a-x)}\)
\(= \frac{2a – 2\sqrt{a²-x²}}{2x}\)
\(= \frac{a – \sqrt{a²-x²}}{x}\)
পুণৰালোচনা Class 9 Maths Q11.
প্ৰমাণ কৰা যেঃ \(\frac{1}{2 + \sqrt{3}} + \frac{2}{\sqrt{5} – \sqrt{3}} + \frac{1}{2 – \sqrt{5}} = \ 0 \)
সমাধানঃ
L.H.S = \(\frac{1}{2 + \sqrt{3}} × \frac{2 – \sqrt{3}}{2 – \sqrt{3}}\) + \(\frac{2}{\sqrt{5} – \sqrt{3}} × \frac{\sqrt{5} + \sqrt{3}}{\sqrt{5}+ \sqrt{3}}\) + \(\frac{1}{2 – \sqrt{5}} × \frac{2 + \sqrt{5}}{2 + \sqrt{5}} \)
\(=\frac{2 – \sqrt{3}}{(2)^2 – (\sqrt{3})^2} \) +\(\frac{2(\sqrt{5} + \sqrt{3})}{(\sqrt{5})^2 – (\sqrt{3})^2}\) +\(\frac{2 + \sqrt{5}}{(2)^2 – (\sqrt{5})^2}\)
\(=\frac{2 – \sqrt{3}}{4 – 3}\) +\(\frac{2(\sqrt{5} + \sqrt{3})}{5 – 3}\) + \(\frac{2 + \sqrt{5}}{4 – 5}\)
\(=\frac{2 – \sqrt{3}}{1}\) + \(\frac{2(\sqrt{5} + \sqrt{3})}{2}\) + \(\frac{2 + \sqrt{5}}{-1}\)
\(= 2 – \sqrt{3}\) + \(\sqrt{5} + \sqrt{3}\) \(- 2 – \sqrt{5}\)
\(= 0 \)
পুণৰালোচনা Class 9 Maths Q12.
\(\sqrt{3}= 1.732\) , \(\sqrt{2}= 1.414\) ধৰি , তলৰ ৰাশিৰ আসন্ন মান উলিওৱাঃ
সমাধানঃ
দিয়া আছে,
\(\sqrt{3}= 1.732\) আৰু \(\sqrt{2}= 1.414\)
(i) \(\frac{1}{\sqrt{3} – \sqrt{2}}\)
\(=\frac{1}{\sqrt{3} – \sqrt{2}} × \frac{\sqrt{3} + \sqrt{2}}{\sqrt{3} + \sqrt{2}}\)
\(= \frac{\sqrt{3} + \sqrt{2}}{(\sqrt{3})^2 – (\sqrt{2})^2}\)
\(= \frac{\sqrt{3} + \sqrt{2}}{3 – 2}\)
\(= \sqrt{3} + \sqrt{2}\)
\(= 1.732 + 1.414\)
\(= 3.146\)
(ii) \(\frac{2}{\sqrt{3} + \sqrt{2}}\)
\(=\frac{2}{\sqrt{3} + \sqrt{2}} × \frac{\sqrt{3} – \sqrt{2}}{\sqrt{3} – \sqrt{2}}\)
\(= \frac{2(\sqrt{3} – \sqrt{2})}{(\sqrt{3})^2 – (\sqrt{2})^2}\)
\(= \frac{2(\sqrt{3} – \sqrt{2})}{3 – 2}\)
\(= 2(\sqrt{3} – \sqrt{2})\)
\(= 2(1.732- 1.414)\)
\(= 2 × 0.318\)
\(= 0.636\)
পুণৰালোচনা Class 9 Maths Q13.
হৰণ কাৰ্য নকৰাকৈ তলৰ পৰিমেয় সংখ্যাবোৰক দশমিকত প্ৰকাশ কৰা ।
(i) \(\frac{7}{25}\)
\(=\frac{7 × 4}{25 × 4}\)
\(=\frac{28}{100}\)
\(=0.28\)
(ii) \(\frac{3}{40}\)
\(=\frac{3 × 25}{40 × 25}\)
\(=\frac{75}{1000}\)
\(=0.075\)
(iii) \(\frac{3}{100}\)
\(=0.03\)
(v) \(\frac{14}{175}\)
\(=\frac{14 ÷ 7}{175 ÷ 7}\)
\(=\frac{2}{25}\)
\(=\frac{2 × 4}{25 × 4}\)
\(=\frac{8}{100}\)
\(= 0.08\)
(iv) \(\frac{23}{5² × 2³}\)
\(=\frac{23 × 5}{5² × 2³ × 5}\)
\(=\frac{115}{5³ × 2³}\)
\(=\frac{115}{10³}\)
\(=\frac{115}{1000}\)
\(= 0.115\)
পুণৰালোচনা Class 9 Maths Q14.
তলৰ শতকৰাবোৰক ভগ্নাংশত প্ৰকাশ কৰাঃ
(i) 53%
\(=\frac{53}{100}\)
(ii) 50%
\(=\frac{50}{100}\)
\(=\frac{1}{2}\)
(iii) \(\frac{1}{2}\%\)
\(=\frac{1}{2×100}\)
\(=\frac{1}{200}\)
(i) 100%
\(=\frac{100}{100}\)
\(= 1\)
(v) 0.01%
\(=\frac{0.01}{100}\)
\(=\frac{1}{10000}\)
পুণৰালোচনা Class 9 Maths Q15.
তলৰ ভগ্নাংশবোৰ শতকৰা ৰূপত লিখাঃ
(i) \(\frac{1}{2}\)
\(=\frac{1}{2} × 100 \%\)
\(= 50 \%\)
(ii) \(\frac{1}{4}\)
\(=\frac{1}{4} × 100 \%\)
\(= 25 \%\)
(iii) \(\frac{3}{20}\)
\(=\frac{3}{20} × 100 \%\)
\(= 3 × 5 \%\)
\(= 15 \%\)
(iv) \(\frac{42}{125}\)
\(=\frac{42}{125} × 100 \%\)
\(=\frac{42}{5} × 4 \%\)
\(=\frac{168}{5} \%\)
\(= 33.6 \%\)
(v) \(0.25\)
\(=0.25 × 100 \%\)
\(= 25 \%\)
(vi) \(1.25\)
\(= 1.25 × 100 \%\)
\(= 125 \%\)
পুণৰালোচনা Class 9 Maths Q16.
কোনো এটা বস্তু 10% লাভত বিক্ৰী কৰা হ’ল । তাৰ কিনাদাম আৰু বেচাদামৰ অনুপাত কি ?
সমাধানঃ
দিয়া আছে, লাভ = 10%
ধৰা হ’ল, বস্তুটোৰ কিনাদাম = 100 টকা
∴ বেচাদাম = কিনাদাম + লাভ
= 100 + 10
= 110 টকা
∴ কিনাদাম : বেচাদাম
= 100 : 110
= 10 : 11
পুণৰালোচনা Class 9 Maths Q17.
30 কণীৰ কিনাদাম, 20 টা কণীৰ বেচাদামৰ সমান । লাভৰ শতকৰা হাৰ কি ?
সমাধানঃ
ধৰা হ’ল, এটা কণীৰ কিনাদাম \(= x \) টকা
এটা কণীৰ বেচাদাম \(= y\) টকা
প্ৰশ্নমতে, \(30x \ = \ 20y\)
\(⇒ y = \frac{30x}{20} = 1.5x\)
∴ এটা কণীত লাভ \(=\) বেচাদাম – কিনাদাম
\(=1.5x \ – \ x = 0.5x\)
∴ লাভৰ শতকৰা হাৰ \(=\) লাভ / কিনাদাম \(× 100 \% \)
\(= \frac{0.5x}{x} × 100 \% \)
\(= 0.5 × 100 \% \)
\(= 50 \% \)
পুণৰালোচনা Class 9 Maths Q18.
এটা বস্তুৰ কিনাদাম 2100 টকা; 10% লাভত বিক্ৰী হ’লে বস্তুটোৰ বেচাদাম দাম কি ?
সমাধানঃ
দিয়া আছে, কিনাদাম \(= 2100 \) টকা
শতকৰা লাভ \(= 10 \% \)
বেচাদাম \(= ? \)
এতিয়া,
বেচাদাম \(= \) কিনাদাম × [(100 + লাভ %)/100]
\(= 2100 × (\frac{100 + 10}{100}) \)
\(= 2100 × \frac{110}{100} \)
\(= 2310 \) টকা
∴ বস্তুটোৰ বেচাদাম 2310 টকা।
পুণৰালোচনা Class 9 Maths Q19.
টকাত 4 টাকৈ নেমু কিনি 20 % লাভত বিক্ৰী কৰিলে । এটা নেমুৰ বিক্ৰী মূল্য কিমান ?
সমাধানঃ
দিয়া আছে, লাভ = 20 %
4 টা নেমুৰ কিনাদাম = 1 টকা
∴ 1 টা নেমুৰ কিনাদাম = \(\frac{1}{4}\) \(= 0.25 \)টকা
∴ 1 টা নেমুত লাভ \(= 0.25 \) টকাৰ 20%
\(= 0.25 × \frac{20}{100} \)
\(= \frac{5}{100} \)
\(= 0.05 \) টকা
∴ এটা নেমুৰ বিক্ৰীমূল্য \(= \) কিনাদাম + লাভ
\(= 0.25 + 0.05 \)
\(= 0.30\) টকা
পুণৰালোচনা Class 9 Maths Q20.
এটা বস্তু 500 টকাত বিক্ৰী কৰিলে 5% লোকচান হয়। এইটো কিমান দামত বেচিলে 5% লাভ হ’লেহেঁতেন ?
সমাধানঃ
প্ৰথম ক্ষেত্ৰতঃ
বেচাদাম \(=500 \) টকা
লোকচান \(=5 \% \)
কিনাদাম \(= ? \)
এতিয়া,
বেচাদাম \(= \) কিনাদাম × [(100 – লোকচান)/100]
\(⇒ 500 = \) কিনাদাম × \(\frac{100-5}{100}\)
\(⇒ 500 = \) কিনাদাম × \(\frac{95}{100}\)
\(⇒ \) কিনাদাম \(= \frac{500 × 100}{95} \)
\(= 526.32 \) টকা
দ্বিতীয় ক্ষেত্ৰতঃ
কিনাদাম \(= 526.32 \) টকা
শতকৰা লাভ \(= 5 \% \)
বেচাদাম \(= ? \)
এতিয়া,
বেচাদাম \(= \) কিনাদাম × [(100 + লাভ )/100]
\(=526.32 × \frac{100 + 5}{100} \)
\(=526.32 × \frac{105}{100} \)
\(=\frac{55263.6}{100} \)
\(=552.636 \)
\(=552.64 \) টকা
পুণৰালোচনা Class 9 Maths Q21.
গ্ৰাহকক আকৰ্ষণ কৰিবলৈ এজন ব্যৱসায়ীয়ে এটা চাৰ্টৰ দামত ক্ৰমে 10%, 10% আৰু 5% ৰেহাই দিয়ে । তিনিওটাৰ সমতুল ৰেহাই কি হ’ব ?
সমাধানঃ
দিয়া আছে,
ৰেহাইৰ হাৰ \(= 10 \%,\ 10 \% \) আৰু \(5\% \)
ধৰা হ’ল,
চাৰ্টটোৰ কিনাদাম \(= 100 \) টকা
এতিয়া,
বেচাদাম \(= \) কিনাদাম × (100 – 10)% × (100 – 10)% × (100 – 5)%
\(= 100 × 90 \% \ × 90 \% \ × 95 \% \)
\(= 100 × \frac{90}{100}\ × \frac{90}{100}\ × \frac{95}{100}\)
\(=\frac{7695}{100}\)
\(=76.95 \) টকা
∴ ৰেহাই \(= \) কিনাদাম \( – \) বেচাদাম
\(= 100 \ – 76.95\)
\(=23.05 \)
∴ ৰেহাইৰ শতকৰা হাৰ \(= 23.05 \% \)
Related Topics
- পুণৰালোচনা R-2
- সংখ্যা প্ৰণালী
- বহুপদ
- স্থানাংক জ্যামিতি
- দুটা চলকযুক্ত ৰৈখিক সমীকৰণ
