Number System Class 9 Assamese Medium Exercise 1.2 :
SEBA Class 9 Maths Exercise 1.2 Solutions: অনুশীলনী 1.2
A solid understanding of the Number System is essential for developing a strong mathematical foundation. To support Class 9 Assamese Medium students, we have provided detailed, step-by-step solutions for Exercise 1.2 (SEBA Class 9 Maths Exercise 1.2).
Our goal is to simplify learning and boost your confidence in this topic. If you have any questions or need further clarification, visit our Doubt Section and ask your queries. Our team is always available to guide you on your learning journey.

Important Notes: SEBA Class 9 Maths Exercise 1.2
(I) অপৰিমেয় সংখ্যা (Irrational Number) : যিবোৰ সংখ্যাক \(\frac{p}{q} \) আৰ্হিত প্ৰকাশ কৰিব নোৱাৰি (য’ত p, q অখণ্ড সংখ্যা আৰু q ≠ 0) সেই সংখ্যাবোৰক অপৰিমেয় সংখ্যা বোলে । উদাহৰণস্বৰূপে- \( \sqrt{2} \) , \( \sqrt{3} \) , \( \sqrt{13} \), \( π \) , 0.10110111011110…. ইত্যাদি ।
(II) বাস্তৱ সংখ্যা (Real numbers) : পৰিমেয় আৰু অপৰিমেয় সংখ্যাবিলাক লগ হৈ গঠন হোৱা সংগ্ৰহটোৱেই হ’ল বাস্তৱ সংখ্যা । বাস্তৱ সংখ্যাৰ সংগ্ৰহটোক R প্ৰতীকৰে বুজোৱা হয় ।
SEBA Class 9 Maths – Number System Solutions Assamese Medium :
- সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.1
- সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.2
- সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.3
- সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.4
- সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.5
- সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.6
- Multiple Choice Questions (MCQ)
SEBA Class 9 Maths Exercise 1.2 Solutions Assamese Medium:
সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.2 সমাধানঃ
SEBA Class 9 Maths Exercise 1.2 Q1.
তলৰ উক্তি বিলাক সত্য নে অসত্য উল্লেখ কৰা । তোমাৰ উত্তৰৰ যথাৰ্থতা প্ৰতিপ্ন্ন কৰা ।
(i) প্ৰতিটো অপৰিমেয় সংখ্যাই এটা বাস্তৱ সংখ্যা ।
\(⇒ \) সত্য, কাৰণ পৰিমেয় আৰু অপৰিমেয় সংখ্যাৰে বাস্তৱ সংখ্যা গঠিত হয় ।
(ii) সংখ্যাৰেখাৰ প্ৰতিটো বিন্দুৱেই \( \sqrt{m} \) আৰ্হিৰ, য’ত m এটা স্বাভাৱিক সংখ্যা।
\(⇒ \) অসত্য, কাৰণ কোনো ঋণাত্মক সংখ্যাই স্বাভাৱিক সংখ্যাৰ বৰ্গমূল নহয়।
(iii) প্ৰতিটো বাস্তৱ সংখ্যাই এটা অপৰিমেয় সংখ্যা ।
\(⇒ \) অসত্য, উদাহৰণ স্বৰূপে 3 এটা বাস্তৱ সংখ্যা কিন্তু অপৰিমেয় নহয় ।
SEBA Class 9 Maths Exercise 1.2 Q2.
সকলো ধনাত্মক অখণ্ড সংখ্যাৰ বৰ্গমূল অপৰিমেয় নে ? যদি নহয় তেনেহ’লে এটা সংখ্যাৰ উদাহৰণ দিয়া যাৰ বৰ্গমূল এটা পৰিমেয় সংখ্যা ।
সমাধানঃ সকলো ধনাত্মক অখণ্ড সংখ্যাৰ বৰ্গমূল অপৰিমেয় নহয় । উদাহৰণ স্বৰূপে; 9 অখণ্ড সংখ্যা কিন্তু \( \sqrt{9} =3 \) এটা পৰিমেয় সংখ্যা ।
SEBA Class 9 Maths Exercise 1.2 Q3.
সংখ্যাৰেখাত কিদৰে \(\sqrt{5} \) ক সূচিত কৰিব পাৰি দেখুওৱা ।
সমাধানঃ সংখ্যাৰেখাত ‘O’ শীৰ্ষবিন্দুটো শূণ্যৰ ওপৰত থকাকৈ OA = 2 একক লোৱা হ’ল আৰু A বিন্দুত AB = 1 একক দৈৰ্ঘ্যৰ লম্ব অঁকা হ’ল।
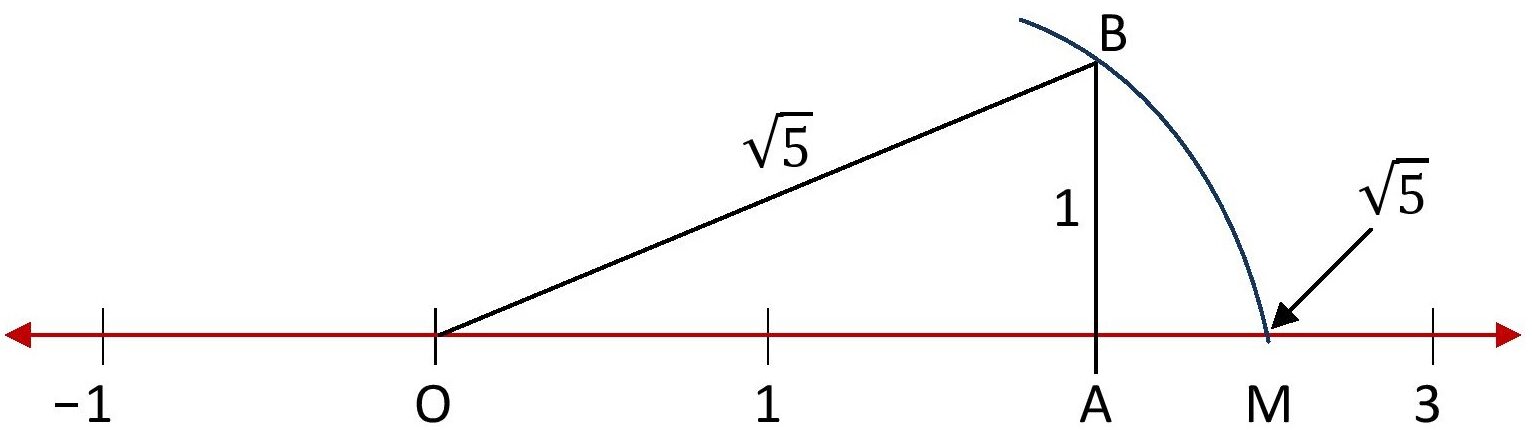
এতিয়া, পাইথাগোৰাচৰ উপপাদ্য প্ৰয়োগ কৰি পাওঁ-
OB = \(\sqrt{OA^2 + AB^2}\)
= \(\sqrt{2^2 + 1^2}\)
= \(\sqrt{4 + 1}\)
= \(\sqrt{5}\)
এতিয়া, ‘O’ বিন্দুক কেন্দ্ৰ কৰি OB = \(\sqrt{5}\) ৰ সমান ব্যাসাৰ্দ্ধ লৈ এটা বৃত্তচাপ অঁকা হ’ল, এই চাপে সংখ্যাৰেখাক M বিন্দুত ছেদ কৰিছে। এই M বিন্দুটোৱেই সংখ্যাৰেখাত \(\sqrt{5}\) ৰ অৱস্থান নিৰ্দেশ কৰে ।
Additional Questions Answer:
SEBA Class 9 Maths Exercise 1.2 Solutions:
সংখ্যাৰেখাত \( \sqrt{2} \) ৰ অৱস্থান নিৰ্ণয় কৰা ।
সমাধান: এটা একক বৰ্গক্ষেত্ৰ OABC লোৱা হ’ল আৰু সংখ্যাৰেখাৰ ওপৰত এনেকৈ অঁকা হ’ল যাতে ‘O’ শীৰ্ষবিন্দুটো শূণ্যৰ ওপৰত থাকে । এতিয়া পাইথাগোৰাচৰ উপপাদ্য ব্যৱহাৰ কৰি পাওঁ-
OB = \(\sqrt{OA^2 + AB^2}\)
= \(\sqrt{1^2 + 1^2}\)
= \(\sqrt{1 + 1}\)
= \(\sqrt{2}\)

এতিয়া, ‘O’ বিন্দুক কেন্দ্ৰ কৰি OB = \(\sqrt{2} \) ৰ সমান ব্যাসাৰ্দ্ধ লৈ এটা বৃত্তচাপ অঁকা হ’ল। এই চাপে P বিন্দুত ছেদ কৰিছে । এই P বিন্দুটোৱেই সংখ্যাৰেখাত \(\sqrt{2} \) ৰ অৱস্থান নিৰ্দেশ কৰে ।
SEBA Class 9 Maths Exercise 1.2 Solutions:
সংখ্যাৰেখাত \(\sqrt{3} \) অৱস্থান নিৰ্ণয় কৰা ।
এটা একক বৰ্গক্ষেত্ৰ OABC লোৱা হ’ল আৰু ‘O’ শীৰ্ষবিন্দুটো শূণ্যৰ ওপৰত থকাকৈ সংখ্যাৰেখাৰ ওপৰত অংকন কৰা হ’ল। ইয়াৰ পৰা পাওঁ-
OB = \(\sqrt{OA^2 + AB^2}\)
= \(\sqrt{1^2 + 1^2}\)
= \(\sqrt{1 + 1}\)
= \(\sqrt{2}\)
আকৌ, এক একক দৈৰ্ঘ্যৰ BD⊥OB ৰেখাখণ্ড অংকন কৰা হ’ল। এতিয়া পাইথাগোৰাচৰ উপপাদ্য প্ৰয়োগ কৰি পাওঁ-
OD = \(\sqrt{OB^2 + BD^2}\)
= \(\sqrt{(\sqrt{2})^2 + 1^2}\)
= \(\sqrt{2 + 1}\)
= \(\sqrt{3}\)
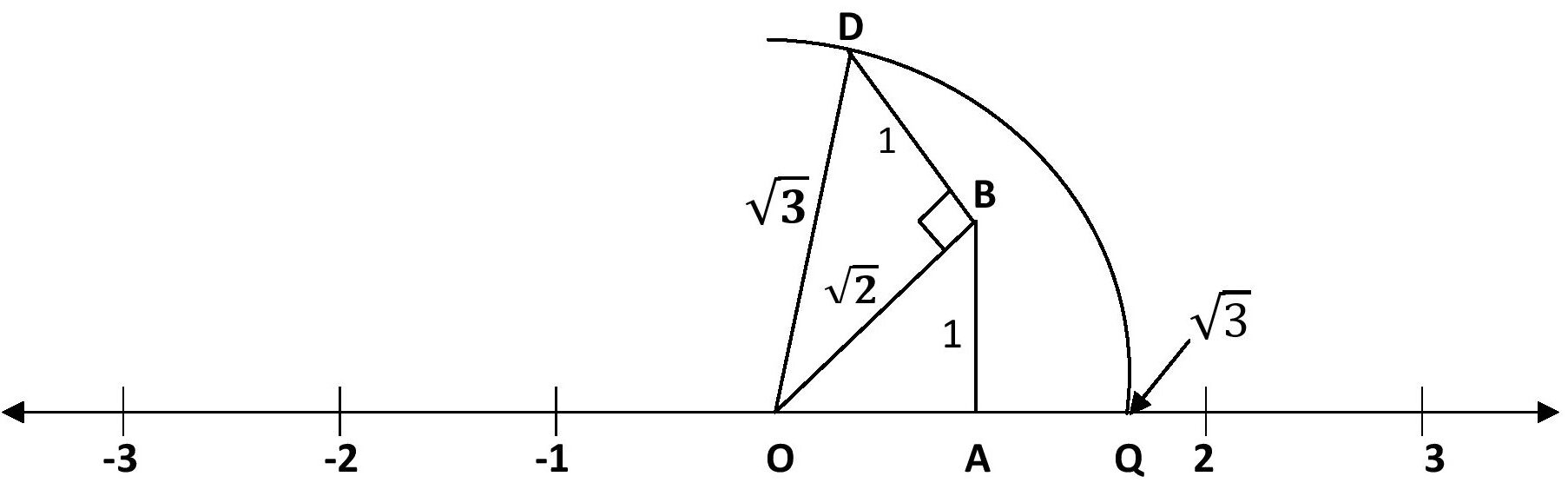
এতিয়া, O বিন্দুক কেন্দ্ৰ কৰি OD = \(\sqrt{3}\) ৰ সমান ব্যাসাৰ্দ্ধ লৈ এটা বৃত্তচাপ অঁকা হ’ল । এই চাপে সংখ্যাৰেখাক Q বিন্দুত ছেদ কৰিছে। এই Q বিন্দুটোৱেই \(\sqrt{3}\) ৰ অৱস্থান নিৰ্দেশ কৰে ।
Related Topics
- পুণৰালোচনা R-1
- পুণৰালোচনা R-2
- বহুপদ
- স্থানাংক জ্যামিতি
- দুটা চলকযুক্ত ৰৈখিক সমীকৰণ
