SEBA Class 9 Maths Exercise 1.3 Solutions:

In this article, we have provided detailed, step-by-step solutions of SEBA Class 9 Maths Excercise 1.3 for Assamese Medium students.

Important Notes: SEBA Class 9 Maths Exercise 1.3

**দশমিক বিস্তৃতি পৰিসমাপ্তঃ- \(\frac{p}{q}\) (q ≠ 0) আৰ্হিৰ সংখ্যা এটাৰ p ক q ৰে হৰণ কৰিলে যদি ভাগশেষ শূণ্য হয়, তেন্তে এই ধৰণৰ সংখ্যা বিলাকৰ দশমিক বিস্তৃতিক পৰিসমাপ্ত (terminating) বুলি কোৱা হয়। উদাহৰণস্বৰূপে- \(\frac{7}{8}\) = 0.875 , \(\frac{1}{2}\) = 0.5 ইত্যাদি।

**দশমিক বিস্তৃতি অপৰিসমাপ্তঃ- \(\frac{p}{q}\) (q ≠ 0) আৰ্হিৰ সংখ্যা এটাৰ p ক q ৰে হৰণ কৰিলে যদি ভাগশেষ কেতিয়াও শূণ্য নহয়, তেন্তে এই ধৰণৰ সংখ্যা বিলাকৰ দশমিক বিস্তৃতিক অবিৰত পৌনঃপুনিক (অপৰিসমাপ্ত) (non-terminating recurring) বুলি কোৱা হয়। উদাহৰণস্বৰূপে- \(\frac{1}{3}\) = 0.3333….., \(\frac{1}{7}\) = 0.142857142857142857……… ইত্যাদি।

**যদি এটা সংখ্যাৰ দশমিক বিস্তৃতি পৰিসমাপ্ত অথবা অবিৰত পুনৰাবৰ্ত্তিত, তেনেহ’লে সেই সংখ্যাটো পৰিমেয়।

**এটা সংখ্যাৰ দশমিক বিস্তৃতি অবিৰত অপুনৰাৱৰ্তিত তেনেহ’লে সেই সংখ্যাটো অপৰিমেয় ।

Class 9 Maths – Number System Solutions Assamese Medium:

সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.1
সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.2
সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.3
সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.4
সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.5
সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.6
Multiple Choice Questions (MCQ)

সংখ্যা প্ৰণালী নৱম শ্ৰেণী অনুশীলনী 1.3 সমাধানঃ

SEBA Class 9 Maths Exercise 1.3 Q1:

তলত দিয়া সংখ্যাবিলাকক দশমিক বিস্তৃতত প্ৰকাশ কৰা আৰু প্ৰতিটোৰে দশমিক বিস্তৃতি কি ধৰণৰ উল্লেখ কৰা-

(i) \(\frac{36}{100} \)

সমাধানঃ

\(\frac{36}{100} \) \(= \) 0.36, দশমিক বিস্তৃতি পৰিসমাপ্ত ।

(ii) \(\frac{1}{11} \)

সমাধানঃ

\(\frac{1}{11} \) \( = \) 0.0909……

\(= \) \(0.\overline{09}\)

যিহেতু, ভাগশেষ পুণৰাবৃত্তি ঘটিছে, গতিকে দশমিক বিস্তৃতি অবিৰত পৌনঃপুনিক ।

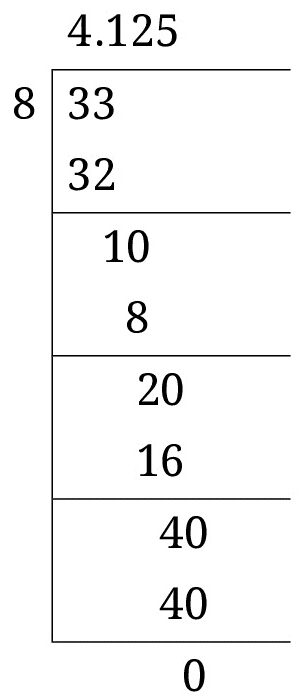
(iii) \(4\frac{1}{8} \)

সমাধানঃ

\(4\frac{1}{8} \) \(= \) \(\frac{33}{8} \)

\(= 4.125 \)

যিহেতু ভাগশেষ 0, গতিকে দশমিক বিস্তৃতি পৰিসমাপ্ত।

(iv) \(\frac{3}{13} \)

সমাধানঃ

\(\frac{3}{13} \) \(= \) 0.230769…..

\(=\) \(0.\overline{230769}\)

যিহেতু ভাগশেষ পুণৰাবৃত্তি ঘটিছে, গতিকে দশমিক বিস্তৃতি অবিৰত পৌনঃপুনিক ।

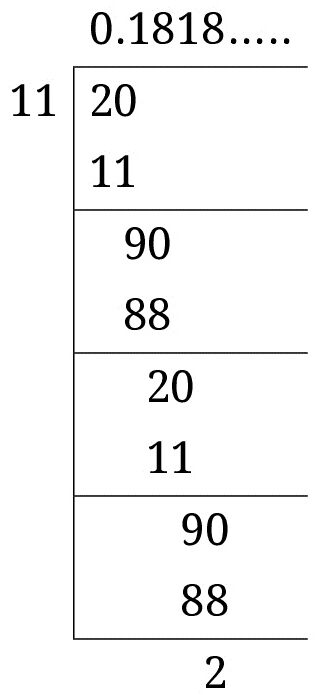
(v) \(\frac{2}{11} \)

সমাধানঃ

\(\frac{2}{11} \) \(= \) 0.181818…….

\(=\) \(0.\overline{18}\)

যিহেতু ভাগশেষ পুণৰাবৃত্তি ঘটিছে, গতিকে দশমিক বিস্তৃতি অবিৰত পৌনঃপুনিক ।

(vi) \(\frac{329}{400} \)

সমাধানঃ

\(\frac{329}{400} \) \(= \) 0.8225

যিহেতু ভাগশেষ 0, গতিকে দশমিক বিস্তৃতি পৰিসমাপ্ত।

SEBA Class 9 Maths Exercise 1.3 Q2:

তোমালোকে জানা যে \(\frac{1}{7} \) \(= \)\(0.\overline{142857}\) । দীঘলীয়া হৰণ নকৰাকৈ \(\frac{2}{7} \), \(\frac{3}{7} \), \(\frac{4}{7} \), \(\frac{5}{7} \),\(\frac{6}{7} \) ৰ দশমিক বিস্তৃতি কি হ’ব ধাৰণা কৰিব পাৰিনে ? যদি পাৰিবা, কেনেকৈ ?

(ইংগিতঃ \(\frac{1}{7} \) ৰ মান উলিয়াওঁতে পোৱা ভাগশেষবোৰ লক্ষ্য কৰা)

সমাধানঃ

দিয়া আছে, \(\frac{1}{7} \) \(= \)\(0.\overline{142857}\)

এতিয়া, \(\frac{2}{7} \) \(= 2 × \) \(\frac{1}{7} \)

\(= 2 × \) \(0.\overline{142857}\)

\(= \) \(0.\overline{285714}\)

\(\frac{3}{7} \) \(= 3 × \) \(\frac{1}{7} \)

\(= 3 × \) \(0.\overline{142857}\)

\(= \) \(0.\overline{428571}\)

\(\frac{4}{7} \) \(= 4 × \) \(\frac{1}{7} \)

\(= 4 × \) \(0.\overline{142857}\)

\(= \) \(0.\overline{571428}\)

\(\frac{5}{7} \) \(= 5 × \) \(\frac{1}{7} \)

\(= 5 × \) \(0.\overline{142857}\)

\(= \) \(0.\overline{714285}\)

\(\frac{6}{7} \) \(= 6 × \) \(\frac{1}{7} \)

\(= 6 × \) \(0.\overline{142857}\)

\(= \) \(0.\overline{857142}\)

SEBA Class 9 Maths Exercise 1.3 Q3.

তলত দিয়াবালাক \(\frac{p}{q} \) আৰ্হিত প্ৰকাশ কৰা, য’ত p আৰু q অখণ্ড সংখ্যা আৰু \(q ≠ 0 \) ।

(i) \(0.\overline{6}\)

সমাধানঃ

ধৰা হ’ল,

\(x = 0.\overline{6}\) ——›(1)

⇒ \(10 \times x = 10\times 0.\overline{6}\)

⇒ \(10x = 6.\overline{6}\)

⇒ \(10x = 6 + 0.\overline{6}\)

⇒ \(10x = 6 + x\) [from (1)]

⇒ \(10x \ – \ x = 6 \)

⇒ \(9x = 6 \)

⇒ \(x = \frac{6}{9}\)

⇒ \(x = \frac{2}{3}\)

(ii) \(0.4\overline{7}\)

সমাধানঃ

ধৰা হ’ল,

\(x = 0.4\overline{7}\) ——›(1)

⇒ \(10 \times x = 10\times 0.4\overline{7}\)

⇒ \(10x = 4.\overline{7}\)

⇒ \(10x = 4.3 + 0.4\overline{7}\)

⇒ \(10x = 4.3 + x\) [from (1)]

⇒ \(10x \ – \ x = 4.3 \)

⇒ \(9x = 4.3 \)

⇒ \(x = \frac{4.3}{9}\)

⇒ \(x = \frac{43}{90}\)

(iii) \(0.\overline{001}\)

সমাধানঃ

ধৰা হ’ল,

\(x = 0.\overline{001}\) ——›(1)

⇒ \(1000 \times x = 1000\times 0.\overline{001}\)

⇒ \(1000x = 1.\overline{001}\)

⇒ \(1000x = 1 + 0.\overline{001}\)

⇒ \(1000x = 1 + x\) [from (1)]

⇒ \(1000x \ – \ x = 1 \)

⇒ \(999x = 1 \)

⇒ \(x = \frac{1}{999}\)

(iv) \(0.\overline{54}\)

সমাধানঃ

ধৰা হ’ল,

\(x = 0.\overline{54}\) ——›(1)

⇒ \(100 \times x = 100\times 0.\overline{54}\)

⇒ \(100x = 54.\overline{54}\)

⇒ \(100x = 54 + 0.\overline{54}\)

⇒ \(100x = 54 + x\) [from (1)]

⇒ \(100x \ – \ x = 54 \)

⇒ \(99x = 54 \)

⇒ \(x = \frac{54}{99}\)

⇒ \(x = \frac{6}{11}\)

(v) \(0.5\overline{9}\)

সমাধানঃ

ধৰা হ’ল,

\(x = 0.5\overline{9}\) ——›(1)

⇒ \(10 \times x = 10\times 0.5\overline{9}\)

⇒ \(10x = 5.\overline{9}\)

⇒ \(10x = 5.4 + 0.5\overline{9}\)

⇒ \(10x = 5.4 + x\) [from (1)]

⇒ \(10x \ – \ x = 5.4 \)

⇒ \(9x = 5.4 \)

⇒ \(x = \frac{5.4}{9}\)

⇒ \(x = \frac{54}{90}\)

⇒ \(x = \frac{3}{5}\)

(vi) \(0.3\overline{45}\)

সমাধানঃ

ধৰা হ’ল,

\(x = 0.3\overline{45}\)

⇒ \(x = 0.3454545……..\) ——›(1)

⇒ \(100 \times x = 100\times 0.3454545……\)

⇒ \(100x = 34.54545……….\)

⇒ \(100x = 34.2 + 0.3454545……..\)

⇒ \(100x = 34.2 + x\) [from (1)]

⇒ \(100x \ – \ x = 34.2 \)

⇒ \(99x = 34.2 \)

⇒ \(x = \frac{34.2}{99}\)

⇒ \(x = \frac{342}{990}\)

⇒ \(x = \frac{19}{55}\)

(vii) \(32.12\overline{35}\)

সমাধানঃ

ধৰা হ’ল,

\(x = 32.12\overline{35}\)

⇒ \(x = 32.12353535……\)

⇒ \(100 \times x = 100\times 32.12353535…..\)

⇒ \(100x = 3212.35353535……\) ——›(1)

⇒ \(100 \times 100x = 100 \times 3212.3535…..\)

⇒ \(10000x = 321235.3535….\) ——›(2)

এতিয়া, (2) − (1)⇒

10000x – 100x = 321235.3535….. – 3212.3535……

⇒ 9900x = 321235 – 3212

⇒ 9900x = 318023

⇒ x = \(\frac{318023}{9900}\)

(viii) \(0.3\overline{7}\)

সমাধানঃ

ধৰা হ’ল,

\(x = 0.3\overline{7}\) ——›(1)

⇒ \(10 \times x = 10\times 0.3\overline{7}\)

⇒ \(10x = 3.\overline{7}\)

⇒ \(10x = 3.4 + 0.3\overline{7}\)

⇒ \(10x = 3.4 + x\) [from (1)]

⇒ \(10x \ – \ x = 3.4 \)

⇒ \(9x = 3.4 \)

⇒ \(x = \frac{3.4}{9}\)

⇒ \(x = \frac{34}{90}\)

⇒ \(x = \frac{17}{45 }\)

SEBA Class 9 Maths Exercise 1.3 Q4.

0.99999……..ক \(\frac{p}{q}\) আৰ্হিত প্ৰকাশ কৰা। তোমাৰ উত্তৰ দেখি আচৰিত হৈছা নেকি ?

সমাধানঃ

ধৰা হ’ল, \( x = 0.99999…….\) →(i)

⇒ \(10 \times x = 10\times 0.99999……\)

⇒ \(10x = 9.9999……….\)

⇒ \(10x = 9 + 0.9999……..\)

⇒ \(10x = 9 + x\) [from (1)]

⇒ \(10x \ – \ x = 9 \)

⇒ \(9x = 9\)

⇒ \(x = \frac{9}{9}\)

⇒ \(x = 1\)

যিহেতু, 0.99999….. সংখ্যাটো 1 ৰ আটাইতকৈ ওচৰৰ সংখ্যা । গতিকে, আমি ক’ব পাৰো যে 0.99999….. = 1 ।

SEBA Class 9 Maths Exercise 1.3 Q5.

\(\frac{1}{17}\) ৰ দশমিক বিস্তৃতিৰ পুনৰাবৰ্ত্তিত গোটটোত আটাইতকৈ বেছি কিমানটা অংক থাকিব ? হৰণ পদ্ধতি অৱলম্বন কৰি উত্তৰৰ সত্যতা পৰীক্ষা কৰা ।

সমাধানঃ \(\frac{1}{17}\) ৰ দশমিক বিস্তৃতিৰ পুনৰাবৰ্ত্তিত গোটটোত আটাইতকৈ বেছি 16 অংক থাকিব ।

\(\frac{1}{17}\) = \(0.\overline{0.0588235294117647}\)

SEBA Class 9 Maths Exercise 1.3 Q6.

যদি p আৰু q অখণ্ড সংখ্যা যাৰ 1 ৰ বাহিৰে অন্য সাধাৰণ উৎপাদক নাই তেনেহ’লে \(\frac{p}{q}\) (q ≠ 0) আৰ্হিত থকা বিভিন্ন পৰিমেয় সংখ্যা লোৱা যিবিলাকৰ দশমিক বিস্তৃতি পৰিসমাপ্ত আৰু পৰ্যবেক্ষণ কৰা । q য়ে কি ধৰ্ম সিদ্ধ কৰিব অনুমান কৰিব পাৰিবানে ?

সমাধানঃ তলত \(\frac{p}{q}\) আৰ্হিৰ কিছুমান পৰিমেয় সংখ্যা লোৱা হ’ল যাৰ দশমিক বিস্তৃতি পৰিসমাপ্ত আৰু p আৰু q ৰ সাধাৰণ উৎপাদক 1 –

\(\frac{3}{5}\) = 0.6, \(\frac{5}{2}\) = 2.5, \(\frac{3}{10}\) = 0.3, \(\frac{7}{20}\) = 0.35

দেখা গ’ল যে q ৰ মৌলিক উৎপাদকীকৰণত কেৱল 2 বা 5 ৰ ঘাত নাইবা দুয়োটাই আছে ।

SEBA Class 9 Maths Exercise 1.3 Q7.

তিনিটা সংখ্যা লিখা যাৰ দশমিক বিস্তৃতি অবিৰত আৰু অপুনৰাৱৰ্তিত (অপৰিসমাপ্ত আৰু অপৌনঃপুনিক) ।

সমাধানঃ দশমিক বিস্তৃতি অবিৰত আৰু অপুনৰাৱৰ্তিত হোৱা তিনিটা সংখ্যা হ’ল-

0.202002000200002……….., 0.05005000500005…………., 0.15015001500015000015……….

SEBA Class 9 Maths Exercise 1.3 Q8.

\(\frac{5}{7}\) আৰু \(\frac{9}{11}\) ৰ মাজত থকা তিনিটা ভিন্ন অপৰিমেয় সংখ্যা উলিওৱা ।

সমাধানঃ

ইয়াত, \(\frac{5}{7}\) = \(0.\overline{714285}\) \(\frac{9}{11}\) = \(0.\overline{81}\)

∴ \(\frac{5}{7}\) আৰু \(\frac{9}{11}\) ৰ মাজত থকা তিনিটা অপৰিমেয় সংখ্যা হ’ল-

0.72072007200072000072…….,

0.75075007500075000075……,

0.78078007800078000078……

SEBA Class 9 Maths Exercise 1.3 Q9.

তলৰ সংখ্যাকেইটাক পৰিমেয় আৰু অপৰিমেয় হিচাপে শ্ৰেণী বিভক্ত কৰাঃ

সমাধানঃ

(i) \(\sqrt{35}\)

\(⇒\) অপৰিমেয় সংখ্যা ।

(ii) \(\sqrt{225}\)

\(⇒\) পৰিমেয় সংখ্যা (কাৰণ, \(\sqrt{225}\) =15)।

(iii) 0.3796

\(⇒\) পৰিমেয় সংখ্যা (যিহেতু,দশমিক বিস্তৃতি পৰিসমাপ্ত)।

(iv) 7.478478………..

\(⇒\) পৰিমেয় সংখ্যা (যিহেতু, দশমিক বিস্তৃতি অবিৰত পৌনঃপুনিক)।

(v) 1.101001000100001……..

\(⇒\) অপৰিমেয় সংখ্যা (যিহেতু, দশমিক বিস্তৃতি অবিৰত অপুনৰাৱৰ্তিত) ।